publications
publications by categories in reversed chronological order. generated by jekyll-scholar.
2024
- CSF
Generalized Information Entropy and Generalized Information DimensionChaos, Solitons & Fractals, Jul 2024The concept of entropy has played a significant role in thermodynamics and information theory, and is also a current research hotspot. Information entropy, as a measure of information, has many different forms, such as Shannon entropy and Deng entropy, but there is no unified interpretation of information from a measurement perspective. To address this issue, this article proposes Generalized Information Entropy (GIE) that unifies entropies based on mass function. Meanwhile, GIE establishes the relationship between entropy, fractal dimension, and number of events. Therefore, Generalized Information Dimension (GID) has been proposed, which extends the definition of information dimension from probability to mass fusion. GIE plays a role in approximation calculation and coding systems. In the application of coding, information from the perspective of GIE exhibits a certain degree of particle nature that the same event can have different representational states, similar to the number of microscopic states in Boltzmann entropy.
@article{zhan2024generalized, title = {Generalized Information Entropy and Generalized Information Dimension}, author = {Zhan, Tianxiang and Zhou, Jiefeng and Li, Zhen and Deng, Yong}, year = {2024}, month = jul, journal = {Chaos, Solitons \& Fractals}, volume = {184}, pages = {114976}, issn = {0960-0779}, doi = {10.1016/j.chaos.2024.114976}, urldate = {2024-06-06}, copyright = {All rights reserved}, langid = {english}, dimensions = {true}, } - ESWA
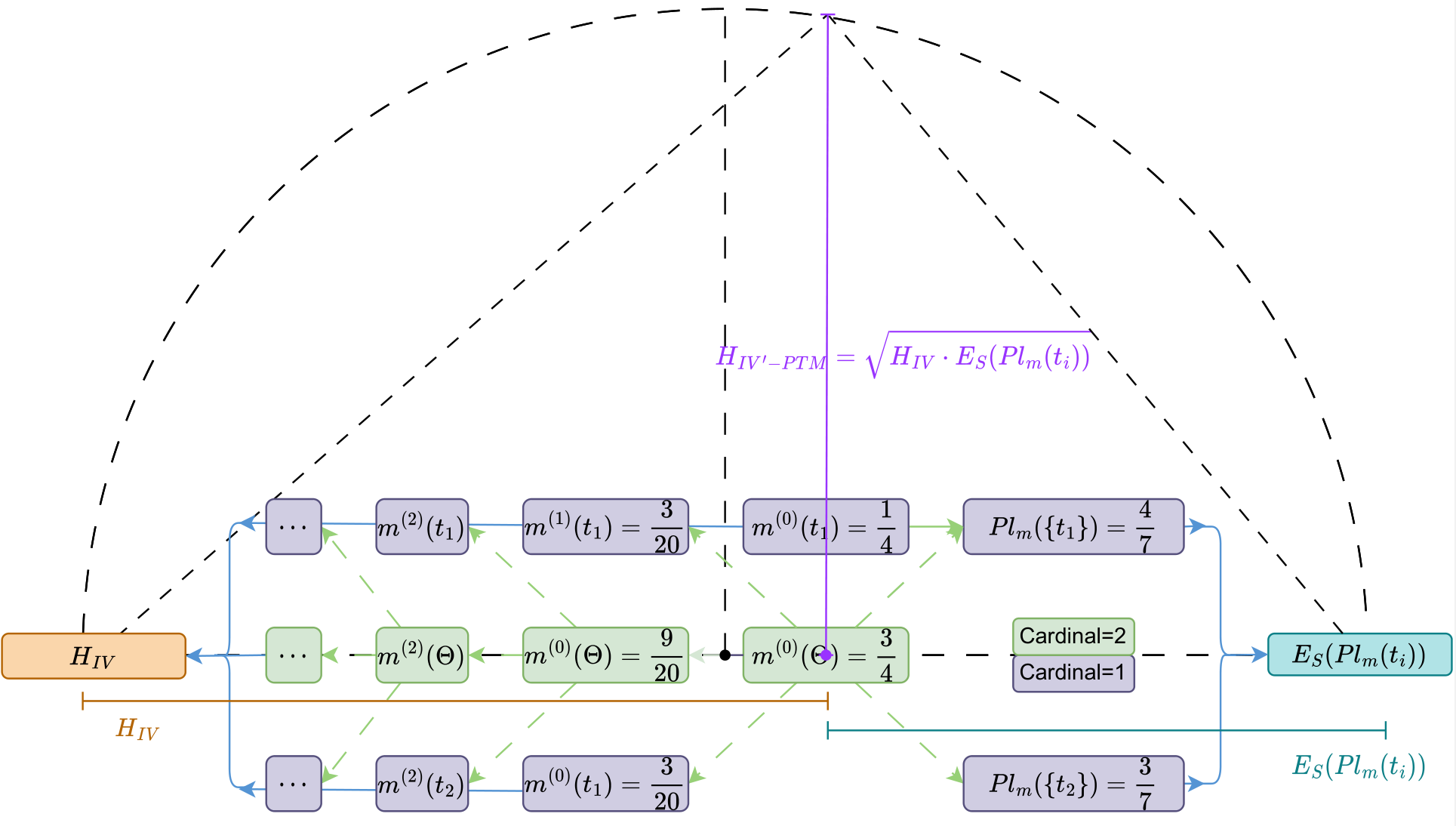An Improved Information Volume of Mass Function Based on Plausibility Transformation MethodExpert Systems with Applications, Mar 2024The information volume of mass function (IVMF) is an effective tool for measuring the uncertainty of basic probability assignments in power sets. However, the current IVMF will yield counterintuitive results when applied to an inconsistent frame of discernment (FOD). To address this issue, an improved IVMF based on plausibility transformation method (PTM) is proposed in this paper. Compared to existing methods, the proposed method yields a more reasonable result in cases where the FOD is inconsistent. Additionally, the proposed IVMF can be viewed as a geometric mean of first-order information volume and higher-order information volume, which can degenerate into Shannon Entropy in a probability distribution. The efficacy and rationality of the proposed IVMF are demonstrated through a series of numerical examples and an application in threat assessment.
@article{zhou2024improved, title = {An Improved Information Volume of Mass Function Based on Plausibility Transformation Method}, author = {Zhou, Jiefeng and Li, Zhen and Deng, Yong}, year = {2024}, month = mar, journal = {Expert Systems with Applications}, volume = {237}, pages = {121663}, issn = {0957-4174}, doi = {10.1016/j.eswa.2023.121663}, copyright = {All rights reserved}, langid = {english}, dimensions = {true}, } - arXiv
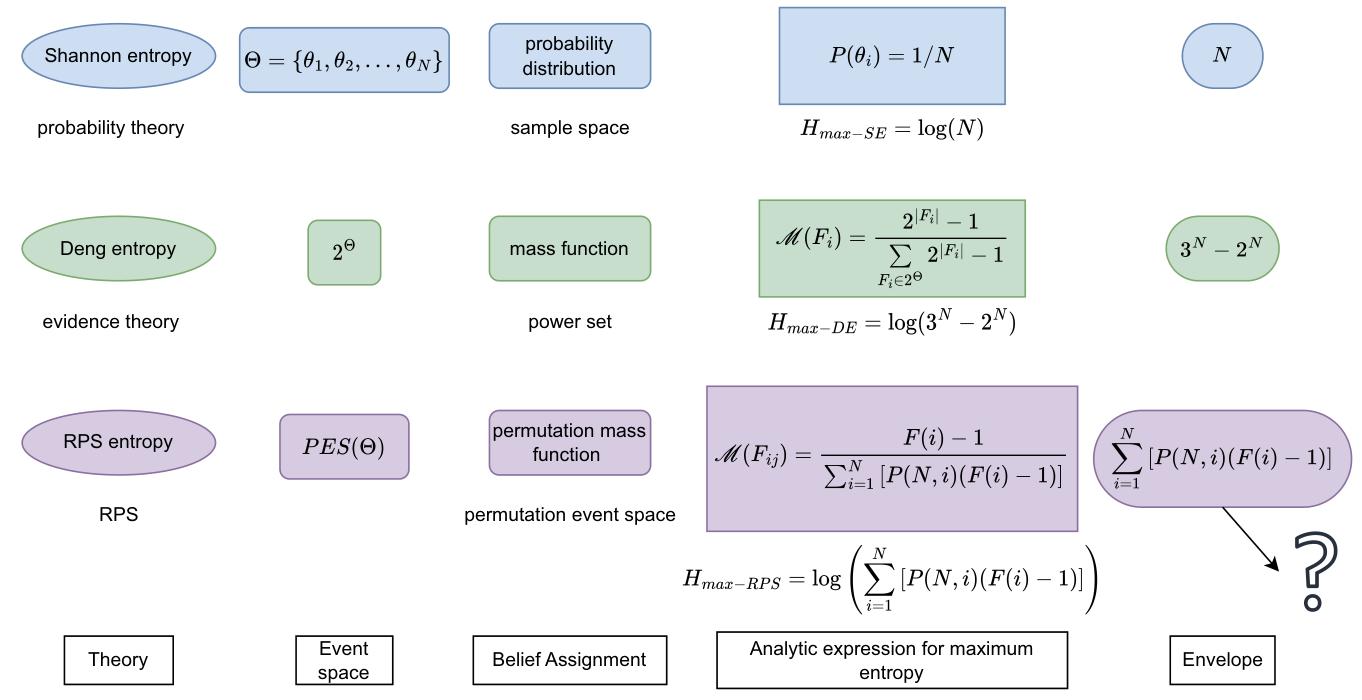Limit of the Maximum Random Permutation Set EntropyMar 2024The Random Permutation Set (RPS) is a new type of set proposed recently, which can be regarded as the generalization of evidence theory. To measure the uncertainty of RPS, the entropy of RPS and its corresponding maximum entropy have been proposed. Exploring the maximum entropy provides a possible way of understanding the physical meaning of RPS. In this paper, a new concept, the envelope of entropy function, is defined. In addition, the limit of the envelope of RPS entropy is derived and proved. Compared with the existing method, the computational complexity of the proposed method to calculate the envelope of RPS entropy decreases greatly. The result shows that when N \to ∞, the limit form of the envelope of the entropy of RPS converges to e \times (N!)^2, which is highly connected to the constant e and factorial. Finally, numerical examples validate the efficiency and conciseness of the proposed envelope, which provides a new insight into the maximum entropy function.
@misc{zhou2024limit, title = {Limit of the {{Maximum Random Permutation Set Entropy}}}, author = {Zhou, Jiefeng and Li, Zhen and Cheong, Kang Hao and Deng, Yong}, year = {2024}, month = mar, number = {arXiv:2403.06206}, eprint = {2403.06206}, primaryclass = {cs, math}, publisher = {arXiv}, doi = {10.48550/arXiv.2403.06206}, urldate = {2024-04-08}, archiveprefix = {arXiv}, copyright = {All rights reserved}, langid = {american}, dimensions = {true}, } - Chaos 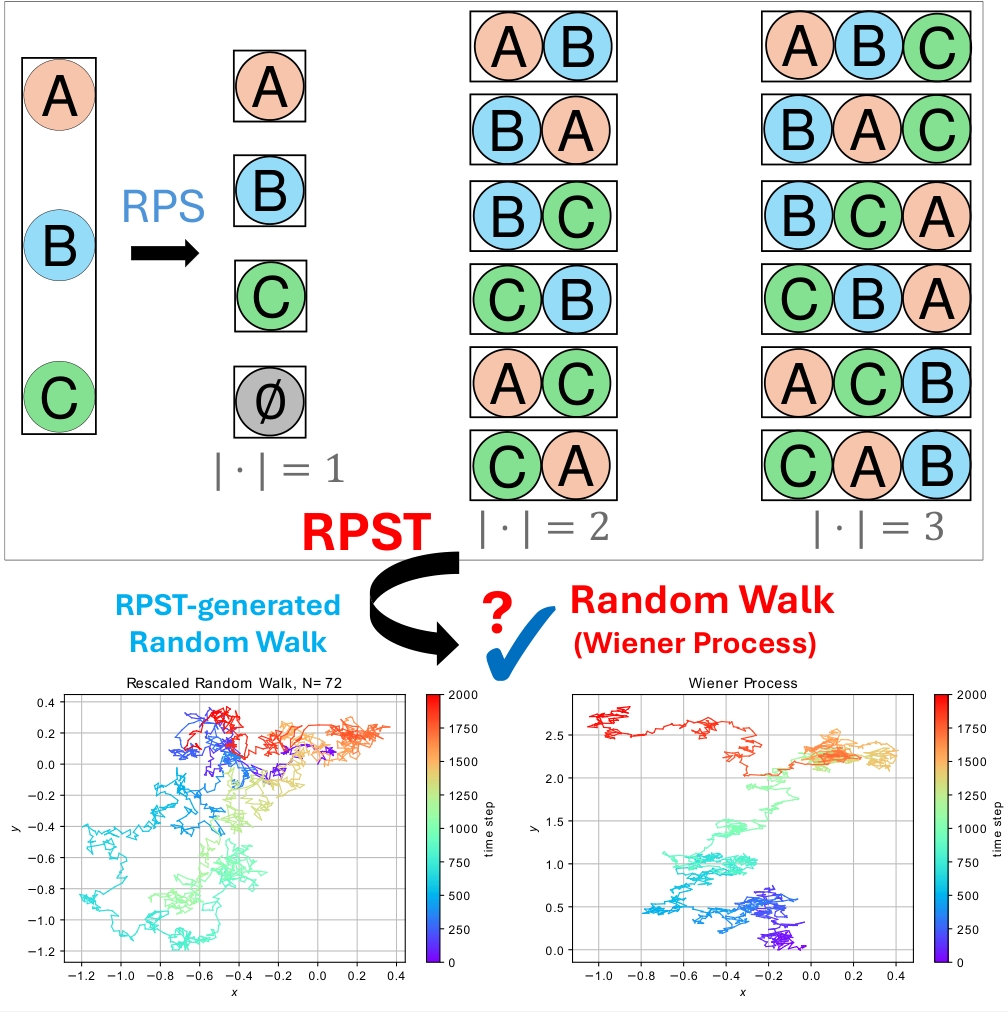Random Walk in Random Permutation Set TheoryChaos: An Interdisciplinary Journal of Nonlinear Science, Sep 2024
Random walk is an explainable approach for modeling natural processes at the molecular level. The random permutation set theory (RPST) serves as a framework for uncertainty reasoning, extending the applicability of Dempster–Shafer theory. Recent explorations indicate a promising link between RPST and random walk. In this study, we conduct an analysis and construct a random walk model based on the properties of RPST, with Monte Carlo simulations of such random walk. Our findings reveal that the random walk generated through RPST exhibits characteristics similar to those of a Gaussian random walk and can be transformed into a Wiener process through a specific limiting scaling procedure. This investigation establishes a novel connection between RPST and random walk theory, thereby not only expanding the applicability of RPST but also demonstrating the potential for combining the strengths of both approaches to improve problem-solving abilities.
@article{zhou2024Random, title = {Random Walk in Random Permutation Set Theory}, author = {Zhou, Jiefeng and Li, Zhen and Deng, Yong}, year = {2024}, month = sep, journal = {Chaos: An Interdisciplinary Journal of Nonlinear Science}, volume = {34}, number = {9}, eprint = {https://pubs.aip.org/aip/cha/article-pdf/doi/10.1063/5.0220154/20174891/093137{\textbackslash}\_1{\textbackslash}\_5.0220154.pdf}, pages = {093137}, issn = {1054-1500}, doi = {10.1063/5.0220154}, dimensions = {true}, }
